- Chương 1 – Hàm số
- Chương 2 – Tọa độ vectơ
- Chương 3 – NGUYÊN HÀM TÍCH PHÂN
- Chương 4 – Thống kê
- Chương 5 – XÁC SUẤT
- Chương 6 – Tổng hợp công thức Oxyz
- BÀI VIẾT LIÊN QUAN
Chương 1 – Hàm số
PHẦN 1 – ĐƠN ĐIỆU VÀ CỰC TRỊ
I. Tính đơn điệu của hàm số (Đồng biến và Nghịch biến)



2. ĐIỂM CỰC TRỊ, GIÁ TRỊ CỰC TRỊ (Cực Đại và Cực Tiểu)
Cực trị là các điểm mà tại đó hàm số chuyển từ tăng sang giảm hoặc ngược lại, tạo thành các “đỉnh núi” hoặc “thung lũng” trên đồ thị.



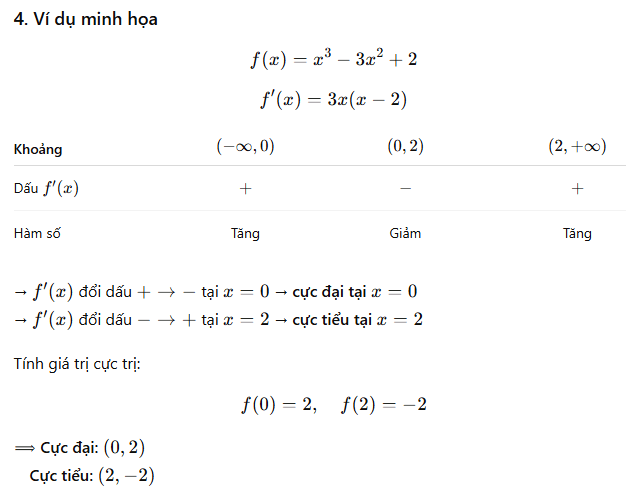

PHẦN 2: Giá trị Lớn nhất, Giá trị Nhỏ nhất và Các Bất Đẳng Thức Cơ Bản
I. Giá trị Lớn nhất và Giá trị Nhỏ nhất (GTLN & GTNN)
Giá trị lớn nhất và nhỏ nhất của hàm số là giá trị cao nhất và thấp nhất mà hàm số đó có thể đạt được trên một tập xác định cho trước.




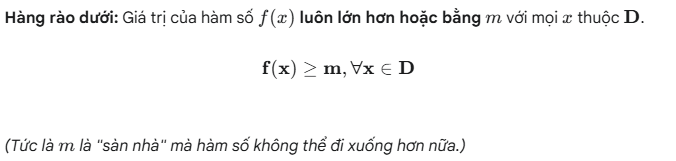


2. Lưu ý Các Bất đẳng thức Quan trọng
Các bất đẳng thức này giúp ta ước lượng GTLN, GTNN của các biểu thức.
2.1. Lưu ý về Giá trị Lớn nhất và Nhỏ nhất (GTLN/GTNN) của hàm số 𝑓𝑓(𝑥𝑥) = asin𝑥𝑥 + 𝑏𝑏 cos𝑥𝑥.


2.2. Các Bất đẳng thức Cơ bản và Ứng dụng
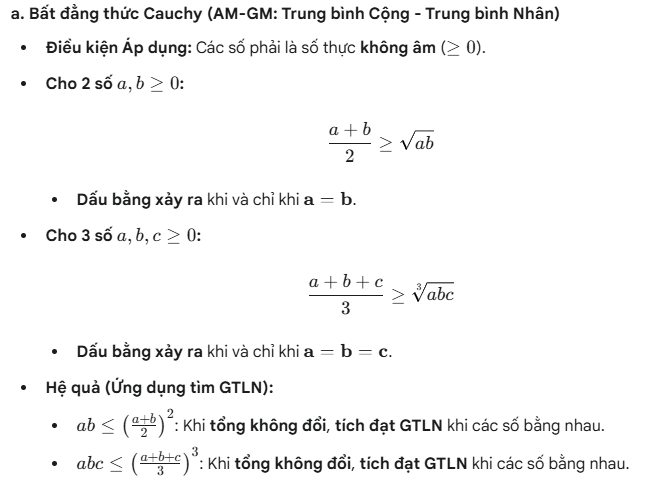


PHẦN 3 – TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
I. Đường Tiệm Cận Ngang
Đường tiệm cận ngang (TCN) là một đường thẳng nằm ngang mà đồ thị hàm số tiến sát tới khi x tiến ra vô cùng.
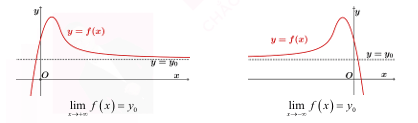


II. Đường Tiệm CậN Đứng
Đường tiệm cận đứng (TCĐ) là một đường thẳng thẳng đứng mà đồ thị hàm số tiến sát tới, nhưng ở đó hàm số lại có giá trị tiến ra vô cùng.







III. Đường Tiệm Cận Xiên
Đường tiệm cận xiên (TCX) là một đường thẳng chéo mà đồ thị hàm số tiến sát tới khi x tiến ra vô cùng.




PHẦN 4 – ĐỒ THỊ HÀM BẬC BA
. I. Kiến thức cần nhớ
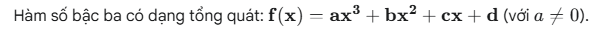

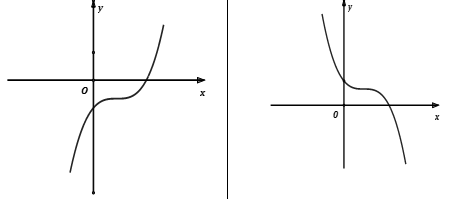
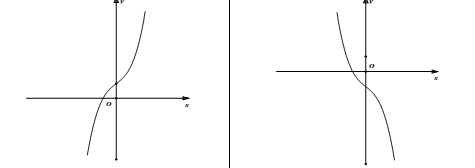



II. Phương trình trình đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số bậc ba
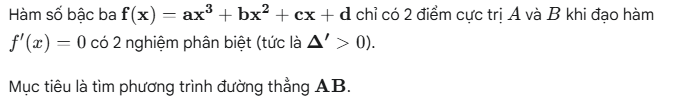

Cơ sở Lý thuyết:


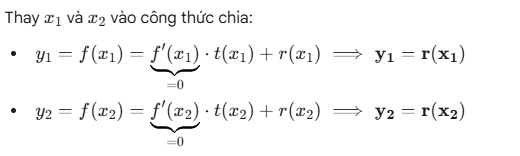




PHẦN 5 – ĐỒ THỊ HÀM SỐ BẬC NHẤT TRÊN BẬC NHẤT

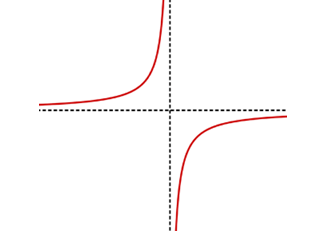



* Đồng biến: Nếu ad−bc>0

* Nghịch biến: Nếu ad−bc<0




PHẦN 6 – ĐỒ THỊ HÀM SỐ BẬC HAI TRÊN BẬC NHẤT






Lưu ý
1. Phương trình đường thẳng đi qua hai điểm cực trị
Cực Trị Hàm Số:
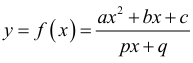
Hàm số xét là:

Hàm số này chỉ có thể có 0 hoặc 2 điểm cực trị.



PHẦN 7 – CÁC PHÉP BIẾN ĐỔI ĐỒ THỊ



PHẦN 8 – SỐ ĐIỂM CỰC TRỊ CỦA HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI
I. Số điểm cực trị của hàm số 𝑦 = |𝑓(𝑥)|
Việc tìm số điểm cực trị của hàm số trị tuyệt đối thường dựa trên đồ thị của hàm số gốc y=f(x).

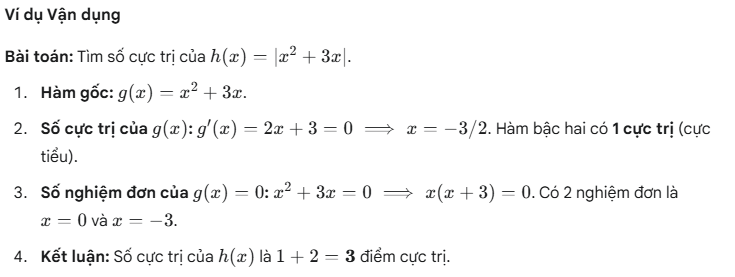





Bình luận về bài viết này